最优二叉查找树:
给定n个互异的关键字组成的序列K=<k1,k2,...,kn>,且关键字有序(k1<k2<...<kn),我们想从这些关键字中构造一棵二叉查找树。对每个关键字ki,一次搜索搜索到的概率为pi。可能有一些搜索的值不在K内,因此还有n+1个“虚拟键”d0,d1,...,dn,他们代表不在K内的值。具体:d0代表所有小于k1的值,dn代表所有大于kn的值。而对于i = 1,2,...,n-1,虚拟键di代表所有位于ki和ki+1之间的值。对于每个虚拟键,一次搜索对应于di的概率为qi。要使得查找一个节点的期望代价(代价可以定义为:比如从根节点到目标节点的路径上节点数目)最小,就需要建立一棵最优二叉查找树。


已知每个关键字以及虚拟键被搜索到的概率,可以计算出一个给定二叉查找树内一次搜索的期望代价。假设一次搜索的实际代价为检查的节点的个数,即所发现的节点的深度加1.计算一次搜索的期望代价等式为:
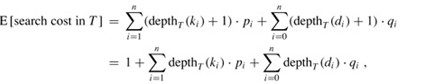
建立一棵二叉查找树,期望搜索代价最小,那么这棵二叉查找树就是最优二叉查找树。
还有:
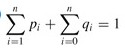
最优子结构:
如果一棵最优二叉查找树T有一棵包含关键字ki,..,kj的子树T',那么这可子树T'对于关键字Ki,...,kj和虚拟键di-1,...dj的子问题也必定是最优的。
给定关键字ki,...,kj,假设kr(i<=r<=j)是包含这些键的一棵最优子树的根。其左子树包含关键字ki,...,kr-1和虚拟键di-1,...,dr-1,右子树包含关键字kr+1,...,kj和虚拟键dr,...dj。我们检查所有的候选根kr,就保证可以找到一棵最优二叉查找树。
一个递归解:
定义e[i,j]为包含关键字ki,...,kj的最优二叉查找树的期望代价,最终要计算的是e[1,n]。
当j = i - 1时,此时子树中只有虚拟键,期望搜索代价为e[i,i - 1] = qi-1.
当j >= i时,需要从ki,...,kj中选择一个根kr,然后分别构造其左子树和右子树。下面需要计算以kr为根的树的期望搜索代价。然后选择导致最小期望搜索代价的kr做根。
子树中每个节点深度都增加1.期望搜索代价增加量为子树中所有概率的总和。
对一棵关键字ki,...,kj的子树,所有概率之和为:
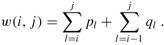
以kr为根的子树的期望搜索代价为:

注意:

因此e[i][j]可以重写为:
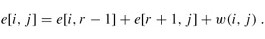
最终可得递归公式:
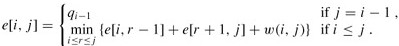
实现代码:
package obst;/** *最优二叉搜索树 *@author wxisme *@time 2015-10-22 下午8:06:04 */public class Solve_obst { public static int[][] e; public static int[][] w; public static int[] p; public static int[] q; public static int[][] root; public static void optional_bst() { int n = p.length+1; e = new int[n+1][n]; w = new int[n+1][n]; root = new int[n][n]; for(int i=1; i<=n; i++) { e[i][i-1] = q[i-1]; w[i][i-1] = q[i-1]; } for(int l=1; l<=n; l++) { for(int i=l; i<=n-l+1; i++) { int j = i+l-1; e[i][j] = Integer.MAX_VALUE; w[i][j] = w[i][j-1] + p[i] +q[j]; for(int r=i; r<=j; r++) { int t = w[i][r-1] + e[r+1][j] + w[i][j]; if(t < e[i][j]) { e[i][j] = t; root[i][j] = r; } } } } }}
将e,w,root对角线旋转到水平方向。如下图:
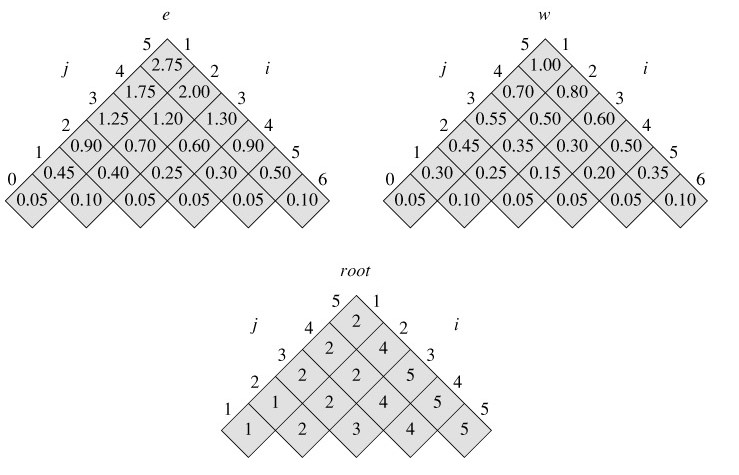
时间复杂度为O(n^3)
FROM 算法导论